Jie Shen : Phase-field models for multiphase complex fluids: modeling, numerical analysis and simulations
- Applied Math and Analysis ( 99 Views )I shall present some recent work on phase-field model for multiphase incompressible flows. We shall pay particular attention to situations with large density ratios as they lead to formidable challenges in both analysis and simulation. I shall present efficient and accurate numerical schemes for solving this coupled nonlinear system, in many case prove that they are energy stable, and show ample numerical results which not only demonstrate the effectiveness of the numerical schemes, but also validate the flexibility and robustness of the phase-field model.
Jiequn Han : Deep Learning-Based Numerical Methods for High-Dimensional Parabolic PDEs and Forward-Backward SDEs
- Applied Math and Analysis ( 108 Views )Developing algorithms for solving high-dimensional partial differential equations (PDEs) and forward-backward stochastic differential equations (FBSDEs) has been an exceedingly difficult task for a long time, due to the notorious difficulty known as the curse of dimensionality. In this talk we introduce a new type of algorithms, called "deep BSDE method", to solve general high-dimensional parabolic PDEs and FBSDEs. Starting from the BSDE formulation, we approximate the unknown Z-component by neural networks and design a least-squares objective function for parameter optimization. Numerical results of a variety of examples demonstrate that the proposed algorithm is quite effective in high-dimensions, in terms of both accuracy and speed. We furthermore provide a theoretical error analysis to illustrate the validity and property of the designed objective function.
Shi Jin : An Eulerian surface hopping method for the Schr\{o}dinger equation with conical crossings
- Applied Math and Analysis ( 104 Views )In a nucleonic propagation through conical crossings of electronic energy levels, the codimension two conical crossings are the simplest energy level crossings, which affect the Born-Oppenheimer approximation in the zeroth order term. The purpose of this paper is to develop the surface hopping method for the Schr\"{o}dinger equation with conical crossings in the Eulerian formulation. The approach is based on the semiclassical approximation governed by the Liouville equations, which are valid away from the conical crossing manifold. At the crossing manifold, electrons hop to another energy level with the probability determined by the Landau-Zener formula. This hopping mechanics is formulated as an interface condition, which is then built into the numerical flux for solving the underlying Liouville equation for each energy level. While a Lagrangian particle method requires the increase in time of the particle numbers, or a large number of statistical samples in a Monte Carlo setting, the advantage of an Eulerian method is that it relies on fixed number of partial differential equations with a uniform in time computational accuracy. We prove the positivity and $l^{1}$-stability and illustrate by several numerical examples the validity and accuracy of the proposed method.
Boyce E. Griffith : Multiphysics and multiscale modeling of cardiac dynamics
- Applied Math and Analysis ( 123 Views )The heart is a coupled electro-fluid-mechanical system. The contractions of the cardiac muscle are stimulated and coordinated by the electrophysiology of the heart; these contractions in turn affect the electrical function of the heart by altering the macroscopic conductivity of the tissue and by influencing stretch-activated transmembrane ion channels. In this talk, I will present mathematical models and adaptive numerical methods for describing cardiac mechanics, fluid dynamics, and electrophysiology, as well as applications of these models and methods to cardiac fluid-structure and electro-mechanical interaction. I will also describe novel models of cardiac electrophysiology that go beyond traditional macroscopic (tissue-scale) descriptions of cardiac electrical impulse propagation by explicitly incorporating details of the cellular microstructure into the model equations. Standard models of cardiac electrophysiology, such as the monodomain or bidomain equations, account for this cellular microstructure in only a homogenized or averaged sense, and we have demonstrated that such homogenized models yield incorrect results in certain pathophysiological parameter regimes. To obtain accurate model predictions in these parameter regimes without resorting to a fully cellular model, we have developed an adaptive multiscale model of cardiac conduction that uses detailed cellular models only where needed, while resorting to the more efficient macroscale equations where those equations suffice. Applications of these methods will be presented to simulating cardiac and cardiovascular dynamics in whole heart models, as well as in detailed models of cardiac valves and novel models of aortic dissection. Necessary physiological details will be introduced as needed.
Siming He : Suppression of Chemotactic collapse through fluid-mixing and fast-splitting
- Applied Math and Analysis ( 132 Views )The Patlak-Keller-Segel equations (PKS) are widely applied to model the chemotaxis phenomena in biology. It is well-known that if the total mass of the initial cell density is large enough, the PKS equations exhibit finite time blow-up. In this talk, I present some recent results on applying additional fluid flows to suppress chemotactic blow-up in the PKS equations. These are joint works with Jacob Bedrossian and Eitan Tadmor.
Katie Newhall : The Causes of Metastability and Their Effects on Transition Times
- Applied Math and Analysis ( 102 Views )Many experimental systems can spend extended periods of time relative to their natural time scale in localized regions of phase space, transiting infrequently between them. This display of metastability can arise in stochastically driven systems due to the presence of large energy barriers, or in deterministic systems due to the presence of narrow passages in phase space. To investigate metastability in these different cases, we take the Langevin equation and determine the effects of small damping, small noise, and dimensionality on the dynamics and mean transition time. In finite dimensions, we show the limit of small noise and small damping do not interchange. In the limit of infinite dimensions, we argue the equivalence of the finitely-damped system and the zero-damped infinite energy Hamiltonian system.
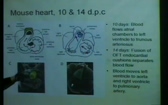
Laura Miller : Scaling effects in heart development: Changes in bulk flow patterns and the resulting forces
- Applied Math and Analysis ( 92 Views )When the heart tube first forms, the Reynolds number describing intracardial flow is only about 0.02. During development, the Reynolds number increases to roughly 1000. The heart continues to beat and drive the fluid during its entire development, despite significant changes in fluid dynamics. Early in development, the atrium and ventricle bulge out from the heart tube, and valves begin to form through the expansion of the endocardial cushions. As a result of changes in geometry, conduction velocities, and material properties of the heart wall, the fluid dynamics and resulting spatial patterns of shear stress and transmural pressure change dramatically. Recent work suggests that these transitions are significant because fluid forces acting on the cardiac walls, as well as the activity of myocardial cells which drive the flow, are necessary for correct chamber and valve morphogenesis.
In this presentation, computational fluid dynamics was used to explore how spatial distributions of the normal forces and shear stresses acting on the heart wall change as the endocardial cushions grow, as the Reynolds number increases, and as the cardiac wall increases in stiffness. The immersed boundary method was used to simulate the fluid-structure interaction between the cardiac wall and the blood in a simplified model of a two-dimensional heart. Numerical results are validated against simplified physical models. We find that the presence of chamber vortices is highly dependent upon cardiac cushion height and Reynolds number. Increasing cushion height also drastically increases the shear stress acting on the cushions and the normal forces acting on the chamber walls.
Yifeng Yu : Random Homogenization of Non-Convex Hamilton-Jacobi Equations in 1d
- Applied Math and Analysis ( 99 Views )I will present the proof of the random homogenization of general coercive Hamiltonian in 1d with the form as H(p,x,\omega)=H(p)+V(x, \omega). Some interesting and complex phenomena associated with non-convex Hamiltonian will also be discussed. This is a joint work with Scott Armstrong and Hung Tran.
Ravi Srinivasan : Kinetic theory for shock clustering and Burgers turbulence
- Applied Math and Analysis ( 94 Views )A remarkable model of stochastic coalescence arises from considering shock statistics in scalar conservation laws with random initial data. While originally rooted in the study of Burgers turbulence, the model has deep connections to statistics, kinetic theory, random matrices, and completely integrable systems. The evolution takes the form of a Lax pair which, in addition to yielding interesting conserved quantities, admits some rather intriguing exact solutions. We will describe several distinct derivations for the evolution equation and, time-permitting, discuss properties of the corresponding kinetic system. This talk consists of joint work with Govind Menon (Brown).
Lin Lin : Elliptic preconditioner for accelerating the self consistent field iteration of Kohn-Sham density functional theory
- Applied Math and Analysis ( 126 Views )Kohn-Sham density functional theory (KSDFT) is the most widely used electronic structure theory for molecules and condensed matter systems. Although KSDFT is often stated as a nonlinear eigenvalue problem, an alternative formulation of the problem, which is more convenient for understanding the convergence of numerical algorithms for solving this type of problem, is based on a nonlinear map known as the Kohn-Sham map. The solution to the KSDFT problem is a fixed point of this nonlinear map. The simplest way to solve the KSDFT problem is to apply a fixed point iteration to the nonlinear equation defined by the Kohn-Sham map. This is commonly known as the self-consistent field (SCF) iteration in the condensed matter physics and chemistry communities. However, this simple approach often fails to converge. The difficulty of reaching convergence can be seen from the analysis of the Jacobian matrix of the Kohn-Sham map, which we will present in this talk. The Jacobian matrix is directly related to the dielectric matrix or the linear response operator in the condense matter community. We will show the different behaviors of insulating and metallic systems in terms of the spectral property of the Jacobian matrix. A particularly difficult case for SCF iteration is systems with mixed insulating and metallic nature, such as metal padded with vacuum, or metallic slabs. We discuss how to use these properties to approximate the Jacobian matrix and to develop effective preconditioners to accelerate the convergence of the SCF iteration. In particular, we introduce a new technique called elliptic preconditioner, which unifies the treatment of large scale metallic and insulating systems at low temperature. Numerical results show that the elliptic preconditioner can effectively accelerate the SCF convergence of metallic systems, insulating systems, and systems of mixed metallic and insulating nature. (Joint work with Chao Yang)
Xiuqing Chen : Global weak solution for kinetic models of active swimming and passive suspensions
- Applied Math and Analysis ( 95 Views )We investigate two kinetic models for active suspensions of rod-like and ellipsoidal particles, and passive suspensions of dumbbell beads dimmers, which couple a Fokker-Planck equation to the incompressible Navier-Stokes or Stokes equation. By applying cut-off techniques in the approximate problems and using compactness argument, we prove the existence of the global weak solutions with finite (relative) entropy for the two and three dimensional models. For the second model, we establish a new compact embedding theorem of weighted spaces which is the key in the compactness argument. (Joint work with Jian-Guo Liu)
Yuri Bakhtin : Noisy heteroclinic networks: small noise asymptotics
- Applied Math and Analysis ( 149 Views )I will start with the deterministic dynamics generated by a vector field that has several unstable critical points connected by heteroclinic orbits. A perturbation of this system by white noise will be considered. I will study the limit of the resulting stochastic system in distribution (under appropriate time rescaling) as the noise intensity vanishes. It is possible to describe the limiting process in detail, and, in particular, interesting non-Markov effects arise. There are situations where this result provides more precise exit asymptotics than the classical Wentzell-Freidlin theory.
Zhennan Zhou : On the classical limit of a time-dependent self-consistent field system: analysis and computation
- Applied Math and Analysis ( 101 Views )We consider a coupled system of Schroedinger equations, arising in quantum mechanics via the so-called time-dependent self-consistent field method. Using Wigner transformation techniques we study the corresponding classical limit dynamics in two cases. In the first case, the classical limit is only taken in one of the two equations, leading to a mixed quantum-classical model which is closely connected to the well-known Ehrenfest method in molecular dynamics. In the second case, the classical limit of the full system is rigorously established, resulting in a system of coupled Vlasov-type equations. In the second part of our work, we provide a numerical study of the coupled semiclassically scaled Schroedinger equations and of the mixed quantum-classical model obtained via Ehrenfest's method. A second order (in time) method is introduced for each case. We show that the proposed methods allow time steps independent of the semi-classical parameter(s) while still capturing the correct behavior of physical observables. It also becomes clear that the order of accuracy of our methods can be improved in a straightforward way.
Fei Lu : Data-based stochastic model reduction for chaotic systems
- Applied Math and Analysis ( 118 Views )The need to deduce reduced computational models from discrete observations of complex systems arises in many climate and engineering applications. The challenges come mainly from memory effects due to the unresolved scales and nonlinear interactions between resolved and unresolved scales, and from the difficulty in inference from discrete data.
We address these challenges by introducing a discrete-time stochastic parametrization framework, through which we construct discrete-time stochastic models that can take memory into account. We show by examples that the resulting stochastic reduced models that can capture the long-time statistics and can make accurate short-term predictions. The examples include the Lorenz 96 system (which is a simplified model of the atmosphere) and the Kuramoto-Sivashinsky equation of spatiotemporally chaotic dynamics.
Sijue Wu : On two dimensional gravity water waves with angled crests
- Applied Math and Analysis ( 91 Views )In this talk, I will survey the recent understandings on the motion of water waves obtained via rigorous mathematical tools, this includes the evolution of smooth initial data and some typical singular behaviors. In particular, I will present our recently results on gravity water waves with angled crests.
Zaher Hani : Out-of-equilibrium dynamics and statistics of dispersive waves
- Applied Math and Analysis ( 94 Views )Out-of-equilibrium behavior is the characteristic feature of the long-time dynamics of nonlinear dispersive equations on compact domain. This means that solutions typically do not exhibit any form of long-time stability near equilibrium solutions or configurations. We shall survey several aspects of this behavior both from a dynamical systems and statistical mechanics point of view.
Chris Bishop : Conformal maps and optimal meshes
- Applied Math and Analysis ( 98 Views )I will describe a linear time algorithm for computing the Riemann map from the unit disk onto an n-gon. The method depends on results from computational geometry (fast computation of the medial axis) and hyperbolic geometry (a theorem of Dennis Sullivan about convex sets in hyperbolic 3-space), as well as classical conformal and quasiconformal theory. Conversely, the fast mapping algorithm implies new results in computational geometry, e.g., (1) quadrilateral meshing for polygons and PSLGs (planar straight line graphs) with optimal time and optimal angle bounds, (2) the first polynomial time algorithm for refining general planar triangulations into non-obtuse triangulations (no angles > 90 degrees; this is desirable for various applications and 90 is the best bound that can be achieved in polynomial time). The talk is intended to be a colloquium-style overview, but I would be happy to discuss more technical details, as requested.
Benedikt Wirth : Optimal fine-scale structures in elastic shape optimization
- Applied Math and Analysis ( 113 Views )A very classical shape optimization problem consists in optimizing the topology and geometry of an elastic structure subjected to fixed boundary loads. One typically aims to minimize a weighted sum of material volume, structure perimeter, and structure compliance (a measure of the inverse structure stiffness). This task is not only of interest for optimal designs in engineering, but e.g. also helps to better understand biological structures. The high nonconvexity of the problem makes it impossible to find the globally optimal design; if in addition the weight of the perimeter is chosen small, very fine material structures are optimal that cannot even be resolved numerically. However, one can prove an energy scaling law that describes how the minimum of the objective functional scales with the model parameters. Part of such a proof involves the construction of a near-optimal design, which typically exhibits fine-scale structure in the form of branching and which gives an idea of how optimal geometries look like. (Joint with Robert Kohn)
Qin Li : Low rankness in forward and inverse kinetic theory
- Applied Math and Analysis ( 113 Views )Multi-scale kinetic equations can be compressed: in certain regimes, the Boltzmann equation is asymptotically equivalent to the Euler equations, and the radiative transfer equation is asymptotically equivalent to the diffusion equation. A lot of detailed information is lost when the system passes to the limit. In linear algebra, it is equivalent to being of low rank. I will discuss such transition and how it affects the computation: mainly, in the forward regime, inserting low-rankness could greatly advances the computation, while in the inverse regime, the system being of low rank typically makes the problems significantly harder.
Jill Pipher : Geometric discrepancy theory: directional discrepancy in 2-D
- Applied Math and Analysis ( 90 Views )Discrepancy theory originated with some apparently simple questions about
sequences of numbers. The discrepancy of an infinite sequence is a
quantitative measure of how far it is from being uniformly distributed.
Precisely, an infinite sequence { a1,a2, ...} is said to be uniformly
distributed in [0, 1] if
lim_{n\to\infty} (1/n|{a1, a2,...an} intersect [s,t]|) = t-s.
If a sequence {ak} is uniformly distributed, then it is also the case
that for all (Riemann) integrable functions f on [0, 1],
lim_{n\to\infty} (1/n\sum_{k=1}^n f(ak))=\int_0^1 f(x)dx.
Thus, uniformly distributed sequences provide good numerical schemes
for approximating integrals. For example, if alpha is any irrational
number in [0, 1], then the fractional part {alphak}:=ak is uniformly
distributed. Classical Fourier analysis enters here, in the form of
Weyl's criterion.
The discrepancy of a sequence with respect to its first n entries is
D({ak},n) := sup_{s
See PDF.
Peter Miller : Integrable Nonlinear Waves and Singular Asymptotics
- Applied Math and Analysis ( 142 Views )This talk will be concerned with nonlinear analogues of the classical methods of analysis for exponential integrals that one uses to study singular limits for linear wave propagation problems solved by Fourier transforms. These analogues apply to nonlinear wave problems that may be treated by a nonlinear analogue of the Fourier transform, the "inverse-scattering transform". We will discuss the use of these techniques to study the semiclassical limit for the focusing nonlinear Schr\"odinger (NLS) equation, and we will also mention some recent work on the modified focusing NLS equation (an equation that tries to make up for shortcomings of the focusing NLS equation arising from modulational instability) and the sine-Gordon equation. The work on sine-Gordon is joint with Robert Buckingham, a recent Duke PhD.
Christoph Ortner : Multi-scale simulation of crystal defects
- Applied Math and Analysis ( 111 Views )PART 1: I will construct a mathematical model of a defect embedded in an infinite homogeneous crystal. I will then establish a regularity result for minimisers, which given the crucial information on which approximation schemes are based. As an elementary application of this framework I will prove convergence rates for two computational schemes: (1) clamped far-field and (2) coupling to harmonic far-field model.
PART 2: The conditions under which the theory of Part 1 holds are separability and locality of the total energy. In Part 2 I will show how for a tight-binding model (a minimalistic electronic structure model) these two condition arise. This analysis raises some interesting (open) questions.
PART 3: Finally, I will use the theory developed in PART 1 and PART 2 to construct and analyse a new family of QM/MM embedding schemes with rigorous error estimates.
Alina Chertock : Numerical Methods for Chemotaxis and Related Models
- Applied Math and Analysis ( 83 Views )Chemotaxis is a movement of micro-organisms or cells towards the areas of high concentration of a certain chemical, which attracts the cells and may be either produced or consumed by them. In its simplest form, the chemotaxis model is described by a system of nonlinear PDEs: a convection-diffusion equation for the cell density coupled with a reaction-diffusion equation for the chemoattractant concentration. It is well-known that solutions of such systems may develop spiky structures or even blow up in finite time provided the total number of cells exceeds a certain threshold. This makes development of numerical methods for chemotaxissystems extremely delicate and challenging task. In this talk, I will present a new family of high-order finite-volume finite-difference methods for the Keller-Segel chemotaxis system and several related models. Applications of the proposed methods to the classical Patlak-Keller-Segel model, its extensions to the two-species case as well as to the coupled chemotaxisfluid system will also be discussed.
Bruce Pitman : Where Are You Going To Go When The Volcano Blows?
- Applied Math and Analysis ( 89 Views )We discuss one approach to determining the hazard threat to a locale due to a large volcanic avalanche. The methodology employed includes large-scale numerical simulations, field data reporting the volume and runout of flow events, and a detailed statistical analysis of uncertainties in the modeling and data. The probability of a catastrophic event impacting a locale is calculated, together with a estimate of the uncertainty in that calculation. By a careful use of simulations, a hazard map for an entire region can be determined. The calculation can be turned around quickly, and the methodology can be applied to other hazard scenarios.

 yes
yes