We consider the basis pursuit problem: find the solution of an underdetermined system $Ax=y$ that minimizes the $l_1$-norm. We formulate a min-max principle (that, as we learned, actually goes back to 1970's) based on a Largange multiplier, and propose an iterative shrinkage-thresholding type algorithm that seems to work quite well. We show that the numerical algorithm converges to the exact solution of the basis pursuit problem. We also discuss its application to array imaging in wave propagation. The analysis is based on ODE techniques, regularization and energy methods. This is a joint work with M. Moscoso, A. Novikov and G. Papanicolaou.

Recently there has been a large class of research that utilizes nonlinear mappings into low dimensional spaces in order to organize potentially high dimensional data. Examples include, but are not limited to, locally linear embedding (LLE), ISOMAP, Hessian LLE, Laplacian eigenmaps, and diffusion maps. In this talk we will focus on the latter, and in particular consider how to generalize diffusion maps to the setting in which we are given a data set that evolves over time or changes depending on some set of parameters. Along with describing the current theory, various synthetic and real world examples will be presented to illustrate these ideas in practice.

The Vicsek model, describing alignment and self-organisation in large systems of self-propelled particles, such as fish schools or flocks of birds, has attracted a lot of attention with respect to its simplicity and its ability to reproduce complex phenomena. We consider here a time-continuous version of this model, in the spirit of the one proposed by P. Degond and S. Motsch, but where the rate of alignment is proportional to the mean speed of the neighboring particles. In the hydrodynamic limit, this model undergoes a phase transition phenomenon between a disordered and an ordered phase, when the local density crosses a threshold value. We present the two different macroscopic limits we can obtain under and over this threshold, namely a nonlinear diffusion equation for the density, and a first-order non-conservative hydrodynamic system of evolution equations for the local density and orientation. (joint work with Pierre Degond and Jian-Guo Liu).

Recent experimental and theoretical research in Bose-Einstein condensation and nonlinear optics have demonstrated novel supersonic, fluid-like phenomena. Shock waves in these and other systems are modeled by a dispersive regularization of Euler's equations, implemented by use of the Whitham averaging technique. Normal and oblique dispersive shock waves (DSWs) connecting two constant states are constructed. Numerical computations of supersonic, dispersive flow over a corner in the special case of systems modeled by the Nonlinear Schrodinger equation (NLS) exhibit stable pattern formation (oblique DSWs) or instability (turbulent-like behavior) depending on the flow parameters. A combination of analytical and computational approaches are used to demonstrate that this change in behavior can be identified with the transition from convective to absolute instability of dark solitons. The linearized NLS behavior about the dark soliton DSW trailing edge is studied in detail to identify the separatrix between convective and absolute instabilities.

The swimming kinematics and trajectories of many microorganisms are altered by the presence of nearby boundaries, be they solid or deformable, and often in perplexing fashion. When an organism's swimming dynamics vary near such boundaries a question arises naturally: is the change in behavior fluid mechanical, biological, or perhaps due to other physical laws? We isolate the first possibility by exploring a far-field description of swimming organisms, providing a general framework for studying the fluid-mediated modifications to swimming trajectories. Using the simplified model we consider trapped/escape trajectories and equilibria for model organisms of varying shape and propulsive activity. This framework may help to explain surprising behaviors observed in the swimming of many microorganisms and synthetic microswimmers.

We consider a droplet spreading on a thin liquid film where both fluids are Newtonian, incompressible, and immiscible. Rather than following the typical asymptotic derivation for a thin film, we formulate the model through a gradient flow approach. The sign of the spreading parameter indicates the spreading behavior (complete or partial spreading) and is a relation between the three interfacial tensions: fluid/air, fluid/drop, and drop/air. We are particularly interested in the case where the spreading parameter is negative. In this case, the drop is expected to spread to a static lens and we find the corresponding equilibrium solution. Finally, we make a comparison between the theoretical model and experimental results.

In this talk, we first give a brief introduction to the discontinuous Galerkin method, which is a finite element method using completely discontinuous basis functions, for solving hyperbolic conservation laws and parabolic and elliptic equations. We will then survey the progress in developing discontinuous Galerkin methods for multiscale problems, in three different approaches, namely using the heterogeneous multiscale method (HMM) framework, using domain decompositions, and using multiscale basis in the discontinuous Galerkin method. Numerical results will be shown to demonstrate the effectiveness of the multiscale discontinuous Galerkin methods.

Compressed sensing, as a signal acquisition technique, has been shown to be highly effective for dimensionality reduction. On the other hand, reconstruction from compressed sensing measurements is highly non-linear and requires digital computers. Thus, quantizing (i.e., digitizing) compressed sensing measurements is an important, albeit under-addressed topic. In this talk, we show that by using $\Sigma\Delta$ quantization instead of the most commonly assumed approach (uniform quantization), a significant reduction in the reconstruction error is possible. In particular, we prove error decay rates of $\lambda^{-c r}$ where $\lambda$ is the ratio of the number of measurements to the sparsity of the underlying signal, and $r$ is the order of the $\Sigma\Delta$ scheme. In addition to the compressed sensing scenario we also consider the quantization of frame expansions, where one collects more measurements than the ambient dimension. We show state of the art results for certain frames (including random frames) and $\Sigma\Delta$ schemes. In particular, we prove error rates of $e^{-c\sqrt{\lambda}}$, where $\lambda$ is the oversampling ratio.

In a nucleonic propagation through conical crossings of electronic energy levels, the codimension two conical crossings are the simplest energy level crossings, which affect the Born-Oppenheimer approximation in the zeroth order term. The purpose of this paper is to develop the surface hopping method for the Schr\"{o}dinger equation with conical crossings in the Eulerian formulation. The approach is based on the semiclassical approximation governed by the Liouville equations, which are valid away from the conical crossing manifold. At the crossing manifold, electrons hop to another energy level with the probability determined by the Landau-Zener formula. This hopping mechanics is formulated as an interface condition, which is then built into the numerical flux for solving the underlying Liouville equation for each energy level. While a Lagrangian particle method requires the increase in time of the particle numbers, or a large number of statistical samples in a Monte Carlo setting, the advantage of an Eulerian method is that it relies on fixed number of partial differential equations with a uniform in time computational accuracy. We prove the positivity and $l^{1}$-stability and illustrate by several numerical examples the validity and accuracy of the proposed method.

We introduce a new particle-based model for self-organized dynamics which, we argue, addresses several drawbacks of the celebrated Cucker-Smale (C-S) model. The new model does not involve any explicit dependence on the number of agents: only their self-driven geometry in phase space enters the model. It lacks, however, the symmetry property, which is the key for the various recent studies of C-S flocking behavior. To this end, we introduce here a new unifying framework to analyze the phenomenon of flocking for a general class of dynamical systems in the presence of non-symmetric influence matrices. In particular, we prove the emerging behavior of flocking in the proposed model, when the pairwise long-range interactions between its agents decays sufficiently slow.

The methodology presented in this paper is based on the notion of active sets, which carries over from the particle to the kinetic and hydrodynamic descriptions. In particular, we discuss the hydrodynamic description of our new model for self-organized dynamics, and we prove its unconditional flocking for sufficiently slowly decaying influence functions.

In mathematics, the study of multilinear algebra is largely limited to properties of a whole space of tensors --- tensor products of k vector spaces, modules, vector bundles, Hilbert spaces, operator algebras, etc. There is also a tendency to take an abstract coordinate-free approach. In most applications, instead of a whole space of tensors, we are often given just a single tensor from that space; and it usually takes the form of a hypermatrix, i.e.\ a k-dimensional array of numerical values that represents the tensor with respect to some coordinates/bases determined by the units and nature of measurements. How could one analyze this one single tensor then? If the order of the tensor k = 2, then the hypermatrix is just a matrix and we have access to a rich collection of tools: rank, determinant, norms, singular values, eigenvalues, condition number, etc. This talk is about the case when k > 2. We will see that one may often define higher-order analogues of common matrix notions rather naturally: tensor ranks, hyperdeterminants, tensor norms (Hilbert-Schmidt, spectral, Schatten, Ky Fan, etc), tensor eigenvalues and singular values, etc. We will discuss the utility as well as difficulties of various tensorial analogues of matrix problems. In particular we shall look at how tensors arise in a variety of applications including: computational complexity, control engineering, mathematical biology, neuroimaging, quantum computing, signal processing, spectroscopy, and statistics.

Frames are nowadays a standard methodology in applied mathematics, computer science, and engineering when redundant, yet stable expansions are required. Sparsity is a new paradigm in signal processing, which allows for significantly reduced measurements yet still highly accurate reconstruction. In this talk, we will focus on the main two links between these exciting, rapidly growing areas. Firstly, the redundancy of a frame promotes sparse expansions of signals, thereby strongly supporting sparse recovery methods such as Compressed Sensing. After providing an overview of sparsity methodologies, we will discuss new results on sparse recovery for structured signals, in particular, which are a composition of `distinct' components. Secondly, in very high dimensions, frame decompositions might be intractable in applications with limited computing budget. This problem can be addressed by requiring sparsity of the frame itself, and we will show how to derive optimally sparse frames. Finally, we will discuss how some of the presented results generalize to the novel notion of fusion frames, which was introduced a few years ago for modeling distributed processing applications.

A chain of pendula connected by nearest neighbor coupling is a near-- integrable system if the coupling is weak. As a consequence of KAM, for most initial data the energy of each pendulum stays near its initial value for all time. We show that these KAM motions coexist with ``diffusing" motions for which the energy can leak from any pendulum to any other pendulum, and it can do so with a prescribed itinerary. This is joint work with Vadim Kaloshin.

The diffusion or adoption of new products (such as fax machines, skype, facebook, Ipad, etc.) is one of the key problems in Marketing research. In recent years, this problem was often studied numerically, using agent-based models (ABMs). In this talk I will focus on analysis of the aggregate diffusion dynamics in ABMs with a spatial structure. In one-dimensional ABMs, the aggregate diffusion dynamics can be explicitly calculated, without using the mean-field approximation. In multidimensional ABMs, we introduce a clusters-dynamics approach, and use it to derive an analytic approximation of the aggregate diffusion dynamics. The clusters-dynamics approximation shows that the aggregate diffusion dynamics does not depend on the average distance between individuals, but rather on the expansion rate of clusters of adopters. Therefore, the grid dimension has a large effect on the aggregate adoption dynamics, but a small-world structure and heterogeneity among individuals have only a minor effect. Our results suggest that the one-dimensional model and the fully-connected Bass model provide a lower bound and an upper bound, respectively, for the aggregate diffusion dynamics in agent-based models with "any" spatial structure. This is joint work with Ro'i Gibori and Eitan Muller

In this talk we present some observations regarding the pressure conditions leading to the vanishing of velocity in the Euler and the Navier-Stokes equations. In the case of axisymmetric 3D Euler equations with special initial data we find that the unformicity condition for the derivatives of the pressure is not consistent with the global regularity.

Taylor-Couette flow provides one of the pre-eminent examples of bifurcation in fluid dynamics. This phrase refers to the flow between concentric rotating cylinders. If the rotation speed is sufficiently rapid, the primary rotary flow around the axis becomes unstable, leading to a steady secondary flow in approximately periodic cells. Assuming infinite cylinders and exact periodicity in his theory, Taylor obtained remarkable agreement with experiment for the onset of instability, agreement that remains unsurpassed in fluid mechanics to this day. This talk is concerned with incorporating the effect of finite-length cylinders into the theory, an issue whose importance was emphasized by Benjamin. Numerous experiments and simulations of the Navier Stokes equations all support to the following, seemingly paradoxical, observations: No matter how long the apparatus, finite-length effects greatly perturb many of the bifurcating flows but, provided the cylinders are long, hardly perturb others. We understand this paradox as a result of symmetry breaking. The relevant symmetry, which is only approximate, is a symmetry between two normal-mode flows with large, and nearly equal, numbers of cells.

A remarkable model of stochastic coalescence arises from considering shock statistics in scalar conservation laws with random initial data. While originally rooted in the study of Burgers turbulence, the model has deep connections to statistics, kinetic theory, random matrices, and completely integrable systems. The evolution takes the form of a Lax pair which, in addition to yielding interesting conserved quantities, admits some rather intriguing exact solutions. We will describe several distinct derivations for the evolution equation and, time-permitting, discuss properties of the corresponding kinetic system. This talk consists of joint work with Govind Menon (Brown).

It is a common expectation in chemistry that a chemical transformation which takes place in the presence of a catalyst must also take place in its absence, though perhaps at a much slower rate. A reaction network will be called ``saturated'' if it satisfies such an expectation. I propose a mathematical definition for saturated networks and show that the associated dynamical systems have no boundary equilibria in positive stoichiometric classes, and are therefore permanent. This result is independent of the specific rates, and generalizes previous results for complete networks by Gnacadja, atomic event-systems by Adleman et al. and constructive networks by Shinar et al. I require no assumption of complex balance or deficiency restrictions. The question of permanence for weakly-reversible reaction networks remains a long-standing open problem.

We will discuss a class of binary measurement matrices having a simple discrete incoherence property. These matrices can be shown to have both useful analytic (i.e., restricted isometry and l1-approximation properties) and combinatorial (i.e., group testing and expander graph related) structure which allows them to be utilized for sparse signal approximation in the spirit of compressive sensing. In addition, their structure allows the actual signal recovery process to be carried out by highly efficient algorithms once measurements have been taken. One application of these matrices and their related recovery algorithms is their application to the development of sublinear-time Fourier methods capable of accurately approximating periodic functions using far fewer samples and run time than required by standard Fourier transform techniques.

It is often desirable to derive an effective stochastic model for the physical process from observational and/or numerical data. Various techniques exist for performing estimation of drift and diffusion in stochastic differential equations from discrete datasets. In this talk we discuss the question of sub-sampling of the data when it is desirable to approximate statistical features of a smooth trajectory by a stochastic differential equation. In this case estimation of stochastic differential equations would yield incorrect results if the dataset is too dense in time. Therefore, the dataset has to sub-sampled (i.e. rarefied) to ensure estimators' consistency. Favorable sub-sampling regime is identified from the asymptotic consistency of the estimators. Nevertheless, we show that estimators are biased for any finite sub-sampling time-step and construct new bias-corrected estimators.

When a fluid layer is heated from below with temperature larger than a certain critical value, the convective motion appears in the fluid. The convection caused by the thermocapillary effect is called Benard-Marangoni heat convection. The thermocapillary effect is the dependence of the surface tension on the temperature. Near a hot spot on a free surface of fluid a thermocapillary tangential stress generates a fluid motion. In this talk the mathematical model system for this convection is explained. The Oberbeck-Boussinesq approximation is used for the system and the upper boundary is a free surface with surface tension which depends on the temperature. After formulating the linearized problem around the conductive state, we derive the resolvent estimates which guarantee the sectorial property. Stationary and Hopf bifurcations (periodic solutions) are proved to exist depending on the parameters (Raylegh and Marangoni numbers).

Conservation equations are at the heart of many interesting and important problems. Examples come from physics, chemistry, biology, traffic and many more. Analytically, hyperbolic equations have a beautiful structure due to the existence of characteristics. These provide the possibility of transforming a conservation PDE into a system of ODE and thus greatly reducing the computational effort required to solve such problems. However, even in one dimension, one encounters problems after a short time.

The most obvious difficulty that needs to be dealt with has to do with the creation of shocks, or in other words, the crossing of characteristics. With a particle based method one would like to avoid a situation when one particle overtakes a neighboring one. However, since shocks are inherent to many hyperbolic equations and relevant to the problems that one would like to solve, it would be good not to ``smooth away'' the shock but rather find a good representation of it and a good solution for the offending particles.

In this talk I will present a new particle based method for solving (one dimensional, scalar) conservation law equations. The guiding principle of the method is the conservative property of the underlying equation. The basic method is conservative, entropy decreasing, variation diminishing and exact away from shocks. A recent extension allows solving equations with a source term, and also provides ``exact'' solutions to the PDE. The method compares favorably to other benchmark solvers, for example CLAWPACK, and requires less computation power to reach the same resolution. A few examples will be shown to illustrate the method, with its various extensions. Due to the current limitation to 1D scalar, the main application we are looking at is traffic flow on a large network. Though we still hope to manage to extend the method to either systems or higher dimensions (each of these extensions has its own set of difficulties), I would be happy to discuss further possible applications or suggestions for extensions.

Boundary value and interface problems for the Laplace equation are often solved by boundary integral methods due to the reduction of dimensionality and its flexibility in domain geometry. However, there are two well-known computational issues with the boundary integral method: (a) evaluation of boundary integrals at points close to domain boundaries usually has low order accuracy; (b) the method typically yields dense coefficient matrices in the resulting discrete systems, which makes the matrix vector multiplication very expensive when the size of the system is very large. In this talk, I will describe a fast accurate boundary integral method for the Laplace boundary value and interface problems. The algorithm uses the high order accurate method proposed by (Beale and Lai 2001) for evaluation of the boundary integrals and applies the fast multipole method for the dense matrix vector multiplication. Numerical results demonstrating the efficiency and accuracy of the method will be presented.

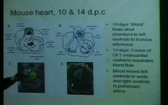
When the heart tube first forms, the Reynolds number describing intracardial flow is only about 0.02. During development, the Reynolds number increases to roughly 1000. The heart continues to beat and drive the fluid during its entire development, despite significant changes in fluid dynamics. Early in development, the atrium and ventricle bulge out from the heart tube, and valves begin to form through the expansion of the endocardial cushions. As a result of changes in geometry, conduction velocities, and material properties of the heart wall, the fluid dynamics and resulting spatial patterns of shear stress and transmural pressure change dramatically. Recent work suggests that these transitions are significant because fluid forces acting on the cardiac walls, as well as the activity of myocardial cells which drive the flow, are necessary for correct chamber and valve morphogenesis.

In this presentation, computational fluid dynamics was used to explore how spatial distributions of the normal forces and shear stresses acting on the heart wall change as the endocardial cushions grow, as the Reynolds number increases, and as the cardiac wall increases in stiffness. The immersed boundary method was used to simulate the fluid-structure interaction between the cardiac wall and the blood in a simplified model of a two-dimensional heart. Numerical results are validated against simplified physical models. We find that the presence of chamber vortices is highly dependent upon cardiac cushion height and Reynolds number. Increasing cushion height also drastically increases the shear stress acting on the cushions and the normal forces acting on the chamber walls.

The purpose of this presentation is to communicate some mathematical and computational issues in sediment transport for open channels. The main topics are: (1) mathematical simulation for surface and subsurface fluid flow, (2) mathematical modeling of sediment transport in open channels as a 2D problem, and (3) numerical methods for fluid flow and sediment transport.

Sleep-wake cycling is an example of switching between discrete states in mammalian brain. Based on the experimental data on the activity of populations of neurons, we develop a mathematical model. The model incorporates several different time scales: firing of action potentials (milliseconds), sleep and wake bout times (seconds), developmental time (days). Bifurcation diagrams in a deterministic dynamical system gives the occupancy time distributions in the corresponding stochastic system. The model correctly predicts that forebrain regions help to stabilize wake state and thus modifies the wake bout distribution.